6步学会朴素贝叶斯算法

2017-11-30

6步学会朴素贝叶斯算法（包含python语言和R语言源码）

摘要

假设你遇到下面这种情况：
你正在研究分类问题，并且你已经生成了你的假设集，创建了特征值，讨论了变量的重要性。在一个小时内，利益相关者希望看到模型的第一个切割。

你会怎么做？你有数以千计个数据点，只有少数变量在你的训练集里面。在这种情况下，如果我是你，我会使用“朴素贝叶斯分类（Navie Bayes）”，相对于其它分类算法，它是非常快的。朴素贝叶斯分类依赖于贝叶斯概率定理来预测未知数据集的类别。
在本文中，我将介绍该算法的基础知识，以便在下次你遇到大型数据集的时候，你可以试用该算法来处理。另外，如果你是Python或R的新手，你应该温习一下这些语言，因为本文将会用这两种语言来实现朴素贝叶斯算法。

要理解贝叶斯推断，必须先理解贝叶斯定理。后者实际上就是计算”条件概率”的公式。

贝叶斯定理

所谓”条件概率”（Conditional probability），就是指在事件B发生的情况下，事件A发生的概率，用P(A|B)来表示。

根据文氏图，可以很清楚地看到在事件B发生的情况下，事件A发生的概率就是P(A∩B)除以P(B)。

因此，

同理可得，

所以，

即

这就是条件概率的计算公式。

全概率公式

由于后面要用到，所以除了条件概率以外，这里还要推导全概率公式。
假定样本空间S，是两个事件A与A’的和。

上图中，红色部分是事件A，绿色部分是事件A’，它们共同构成了样本空间S。
在这种情况下，事件B可以划分成两个部分。

即

在上一节的推导当中，我们已知

所以，

这就是全概率公式。它的含义是，如果A和A’构成样本空间的一个划分，那么事件B的概率，就等于A和A’的概率分别乘以B对这两个事件的条件概率之和。
将这个公式代入上一节的条件概率公式，就得到了条件概率的另一种写法：

对条件概率公式进行变形，可以得到如下形式：

我们把P(A)称为”先验概率”（Prior probability），即在B事件发生之前，我们对A事件概率的一个判断。P(A|B)称为”后验概率”（Posterior probability），即在B事件发生之后，我们对A事件概率的重新评估。P(B|A)/P(B)称为”可能性函数”（Likelyhood），这是一个调整因子，使得预估概率更接近真实概率。
所以，条件概率可以理解成下面的式子：

1	后验概率　＝　先验概率ｘ调整因子

这就是贝叶斯推断的含义。我们先预估一个”先验概率”，然后加入实验结果，看这个实验到底是增强还是削弱了”先验概率”，由此得到更接近事实的”后验概率”。
在这里，如果”可能性函数”P(B|A)/P(B)>1，意味着”先验概率”被增强，事件A的发生的可能性变大；如果”可能性函数”=1，意味着B事件无助于判断事件A的可能性；如果”可能性函数”<1，意味着”先验概率”被削弱，事件A的可能性变小。

什么是贝叶斯算法？

贝叶斯算法一种基于贝叶斯定理的分类技术，具有独立于预测因子的假设。简而言之，朴素贝叶斯分类器假设类中特定特征和其它特征的存在无关。例如，一个水果如果是红色，圆形的，并且直径约3英尺，则这个水果可以被认为是红色苹果。即使这些特征依赖于彼此或者依赖于其它特征的存在，所有的这些特征独立的贡献了这个水果是苹果的可能性，这就是为什么它被称为“朴素”的原因。
朴素贝叶斯模型很容易构建，特别适用于非常大的数据集。除了简单性，众所周知，朴素贝叶斯甚至胜过高度复杂的分类方法。
贝叶斯定理提供了一种从P(c),P(x)和P(x|c)计算后验概率P(c|x)的方法。看下面的公式：
bayes
以上：

P（c|x）是给定预测变量（x，属性）的类（c，target）的后验概率。【即在看到新数据后，我们要计算的该假设的概率】
P（c）是类的先验概率。【即在得到新数据前某一假设的概率】
P（x | c）是预测器给定类的概率的可能性。【该假设下得到这一数据的概率，称为似然度】
P（x）是预测器的先验概率。【在任何假设下得到这一数据的概率，称为标准化常量】

贝叶斯算法是如何工作的？

让我们用一个例子来理解它。下面我有一个天气和相应的目标变量“玩”（建议玩的可能性）的训练数据集。现在，我们需要根据天气状况来分类玩家是否玩游戏。让我们按照下面的步骤来执行它。

步骤1：将数据集转换为频率表

步骤2：通过查找概率如“阴天的概率= 0.29”和“播放的概率为0.64”来创建“似然”表。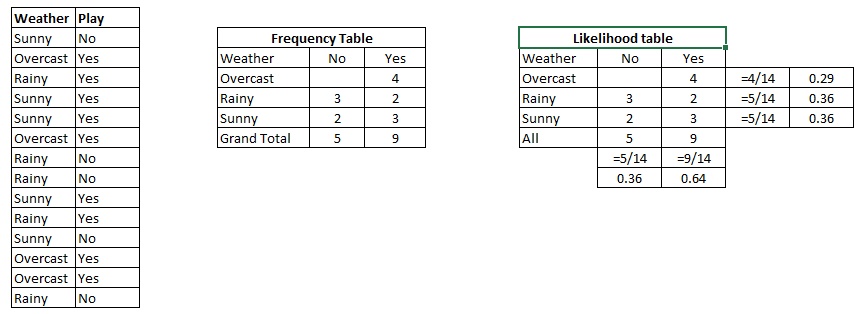
bayes2

步骤3：现在，使用朴素贝叶斯方程来计算每个类别的后验概率。后验概率最高的是预测的结果。
问题：如果天气晴朗，玩家将会玩。这种说法是正确的吗？

我们可以使用上面讨论的后验概率的方法来解决这个问题。

P(是|晴天)= P(晴天|是)*P(是)/ P(晴天)

这里我们有P（晴天|是）= 3/9 = 0.33，P（晴天）= 5/14 = 0.36，P（是）= 9/14 = 0.64

现在，P（是| 晴天）= 0.33 * 0.64 / 0.36 = 0.60，其概率较高。

朴素贝叶斯使用类似的方法来预测基于各种属性的不同类别的概率，这个算法主要用于文本分类和多类问题。

朴素贝叶斯算法的优点和缺点是什么？

优点：

预测测试数据集的类别是容易且快速的,它在多分类预测中也表现良好
当独立性假设成立时，朴素贝叶斯分类器与逻辑回归等其他模型相比表现更好，而且需要更少的训练数据。
与数值变量（s）相比，它在分类输入变量的情况下表现良好。数值变量是正态分布假设（正态曲线图，这是一个强有力的假设）。

缺点：

如果分类变量在测试数据集里面有类别，但在训练数据集中未观察到该类别，则模型将分配0（零）概率，并且将不能进行预测。这通常被称为“
零概率”。为了解决这个问题，我们可以使用平滑技术。最简单的平滑技术之一被称为拉普拉斯评估。
另一方面，朴素贝叶斯（Bayes）也被称为不好的估计器，所以来自predict_proba的概率输出不应该被过于重视。
朴素贝叶斯的另一个局限是独立预测因子的假设。在现实生活中，我们得到一组完全独立的预测变量几乎是不可能的。

朴素贝叶斯算法的四种应用

实时预测：朴素贝叶斯是一个热切的学习分类器，它肯定是快速的。因此，它可以用于实时预测。
多类预测：这种算法也是众所周知的多类预测功能。这里我们可以预测多个目标变量类别的概率。
文本分类/垃圾邮件过滤/情感分析：主要用于文本分类的朴素贝叶斯分类器（由于更好的结果在多类问题和独立性规则）比其他算法具有更高的
成功率。因此，它被广泛用于垃圾邮件过滤（识别垃圾邮件）和情感分析（在社交媒体分析中，识别客户积极和消极的情绪）
推荐系统：朴素贝叶斯分类器和协作过滤一起构建推荐系统，该系统使用机器学习和数据挖掘技术来过滤看不见的信息并预测用户是否喜欢给定
的资源。

用python语言构建基本的朴素贝叶斯模型的步骤

再次，scikit学习（python库）将使用python语言在这里帮助建立一个朴素贝叶斯模型。在scikit学习库中有三种类型的朴素贝叶斯模型：

高斯（Gaussian）：它用于分类，它假设特征遵循正态分布。
多项式(Multinomial)：用于离散计数。比如说，我们有一个
文本分类问题。在这里，我们可以进一步考虑伯努利实验，而不是“在文件中出现的单词”，而是“统计单词在文档中出现的频率”，你可以将其视
为“观察结果数x_i在n次试验中的次数“。
伯努利(Bernoulli)：如果你的特征向量是二进制的（即零和一），二项式模型是有用的。一个应用是文本分类，词袋模型，其中1s＆0s分别是“
单词出现在文档中”和“单词不出现在文档中”。

根据你的数据集，你可以选择任何上面讨论的模型。以下是高斯模型的例子。

Python 代码

#Import Library of Gaussian Naive Bayes model
from sklearn.naive_bayes import GaussianNB
import numpy as np
#assigning predictor and target variables
x= np.array([[-3,7],[1,5], [1,2], [-2,0], [2,3], [-4,0], [-1,1], [1,1], [-2,2], [2,7], [-4,1], [-2,7]])
Y = np.array([3, 3, 3, 3, 4, 3, 3, 4, 3, 4, 4, 4])

#Create a Gaussian Classifier
model = GaussianNB()
# Train the model using the training sets 
model.fit(x, y)
#Predict Output 
predicted= model.predict([[1,2],[3,4]])
print predicted
Output: ([3,4])

R 代码

require(e1071) #Holds the Naive Bayes Classifier
Train <- read.csv(file.choose())
Test <- read.csv(file.choose())
#Make sure the target variable is of a two-class classification problem only
levels(Train$Item_Fat_Content)
model <- naiveBayes(Item_Fat_Content~., data = Train)
class(model) 
pred <- predict(model,Test)
table(pred)

上面我们看了朴素贝叶斯模型，可以通过调整参数和智能处理假设来提高这个基本模型的能力。我们来看看改进朴素贝叶斯模型性能的方法。我建议你阅读这个文档，解关于使用朴素贝
叶斯的文本分类的更多细节。

提高朴素贝叶斯模型的方法

以下是提高Naive Bayes模型功能的一些建议：

如果连续性特征不具有正态分布，则应采用变换或不同的方法将其转换为正态分布。
如果测试数据集具有零频率问题，则应用平滑技术“拉普拉斯修正”来预测测试数据集的类别。
删除相关特征，因为高度相关的特征在模型中被投票两次，并且可能导致过度膨胀的重要性。
朴素贝叶斯分类器参数调整的选项是有限的，比如alpha = 1来平滑，fit_prior = [True | False]来学习类别先验概率，还有其他一些选项（请看这里的细节）。我建议把重点放在数据的预处理和特征选择上。
你可能会认为应用一些分类器组合技术，如集合，装袋和提高，但这些方法将无济于事。实际上，“集合，提升，装袋”不会有帮助，因为它
们的目的是减少变化。朴素贝叶斯没有任何变化可以最小化。

结束笔记

在本文中，我们看了一个主要用于分类的监督机器学习算法“朴素贝叶斯”。恭喜，如果你已经完全理解这篇文章，你已经迈入掌握这个算法的第一步。从这里开始，你需要的是练习。

此外，我建议您在应用朴素贝叶斯算法之前更多地关注数据预处理和特征选择。

你觉得这篇文章有帮助吗？请在下面的评论部分分享您的意见/想法。

原文

Chaoping Ding